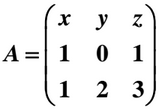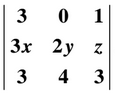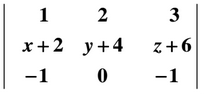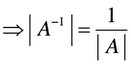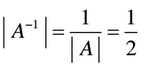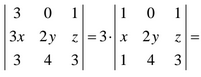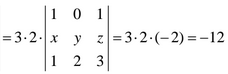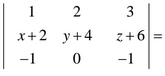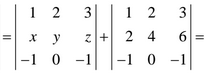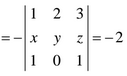Septiembre 2014: Opción B
Ejercicio 3
Sabiendo que el determinante de la matriz A es 2, calcula los siguientes determinantes indicando, en cada caso, las propiedades que utilices:
a) Calcula det(3A)
b) Calcula det(A-1)
c) Calcula el siguiente determinante
d) Calcula el siguiente determinante
Solución
a) Si An es una matriz cuadrada de orden n, sabemos que se cumple que |k*A| = kn *|A|; en nuestro caso como A es una matriz de orden 3, tenemos que la solución es:
|3A| = (3)3 * |A|=27 *2=54
b) Después de lo que hemos aprendido en la teoría sabemos que,
Por lo tanto la solución es la siguiente:
c) En el 1er y 2º paso hemos aplicado la 6ª Propiedad de los determinantes que dice: «Si se multiplica un determinante por un número real, hay que multiplicar por dicho número sólo y exclusivamente una línea (fila o columna) del determinante.»
En el 3er paso hemos aplicado la 4ª Propiedad que dice: “Si se intercambian entre sí dos líneas (filas o columnas) de un determinante, su valor cambia de signo”. La solución es:
d) En el 1er paso hemos aplicado la 7ª Propiedad que dice: «Si todos los elementos de una línea (fila o columna) están formados por dos sumandos, dicho determinante se descompone en la suma de dos determinantes en los que las demás líneas (filas o columnas) permanecen sin cambios», además se hemos aplicado la 2ªa Propiedad que dice: «Tiene dos líneas (filas o columnas) iguales, el determinante vale 0«
Por lo tanto la solución es:
Recuerda la teoría:
>> Apartado 3.5 "Propiedades Determinantes"
>> Apartado 3.6 "Matriz Inversa"
Sigue jugando y ganando confianza haciendo los Ejercicios de Selectividad Matemáticas II!!!