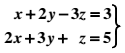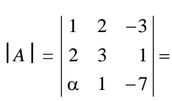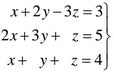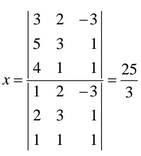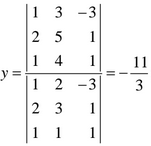Junio 2014: Opción A

Ejercicio 3

Considera el siguiente sistema de ecuaciones lineales

a) Calcula α de manera que al añadir una tercera ecuación de la forma αx+y-7z=1 el sistema resultante tenga las mismas soluciones que el original.

b) Calcula las soluciones del sistema dado tales que la suma de los valores de las incógnitas sea 4.

Solución

a) El sistema que nos dan es un sistema compatible indeterminado y tiene infinitas soluciones, para que tenga las mismas soluciones al añadirle la nueva ecuación el rango de la matriz de los coeficientes tiene que valer 2, luego, el determinante tiene que valer 0.

Calculamos el determinante de la matriz de los coeficientes y lo igualamos a 0.

Calculamos los rangos de la matriz de los coeficientes y de la matriz ampliada del sistema y obtenemos la siguiente solución:

α=0

R(A)=2

R(M)=2

Sistema Compatible Indeterminado

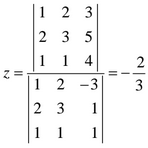
b) Nos piden que se cumpla la siguiente relación en la ecuación, x+y+z=4, por lo tanto resolvemos el siguiente sistema

Resolvemos el sistema por el método de Cramer y obtenemos la siguiente solución:

Recuerda la teoría:
     >> Apartado 3.2 "Regla de Sarrus"
     >> Apartado 3.7 "Calculo Rango"

Sigue jugando y ganando confianza haciendo los Ejercicios de Selectividad Matemáticas II!!! "Septiembre 2014: Opcion B: Ejercicio 3"