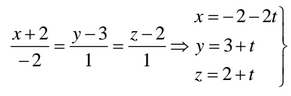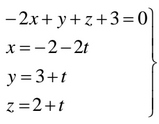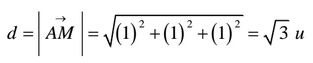Junio 2014: Opción A

Ejercicio 4

Considera la recta r que pasa por los puntos A(1,0, 1) y B( 1,1,0).

a) Halla la ecuación de la recta s paralela a r que pasa por C(–2,3,2).

b) Calcula la distancia de r a s.

Solución

a) Se calcula el vector director de la recta r :

Como las rectas son paralelas, el vector director de s es AB(-2,1,1), por lo tanto la ecuación de la recta s es:

b) Como las rectas son paralelas, su distancia se obtiene conociendo la distancia del punto A=(1,0,–1) a la recta s. Para ello se calcula un plano perpendicular a la recta s que pase por el punto A=(1,0,–1).

A continuación se calcula el punto de corte del plano y la recta s, para ello se resuelve el siguiente sistema,

Por tanto, el punto de corte es el siguiente:

y la distancia entre las rectas viene dada por el módulo del vector siguiente:

Finalmente la solución es:

Recuerda la teoría:
     >> Apartado 7.3 "Distancia entre puntos, rectas y planos"

Sigue jugando y ganando confianza haciendo los Ejercicios de Selectividad Matemáticas II!!!