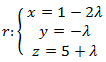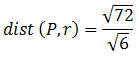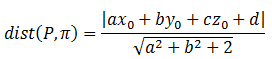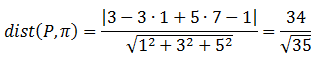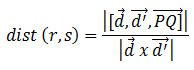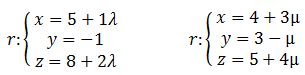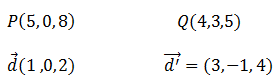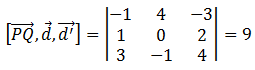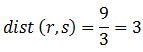Tema 7: Problemas métricos

7.3.- Distancia entre puntos,  rectas y planos

7.3.1.- Distancia entre dos puntos

La distancia entre dos puntos P₁(x₁, y₁, z₁) y P₂(x₂, y₂, z₂) se calcula como:

• Ejemplo:

La distancia entre  P (5, -1, 7) y Q (4, -5, 11) es:

7.3.2.- Distancia entre un punto y una recta

La distancia entre un punto P y una recta r de vector director , se puede calcular mediante la siguiente expresión:

• Ejemplo:

Calcular la distancia entre el punto  P (5, -1, 7) y la recta r de la ecuación:

El vector director de r es  d(-2,-1,1) y un punto de r ,haciendo λ=0  ,es R (-2,-1,1) . Por tanto:

7.3.3.- Distancia de un punto a un plano

La distancia de un punto P(x₀, y₀, z₀) a un plano π: ax+by+cz=0  puede calcularse a través de la siguiente expresión:

• Ejemplo:

Calcular la distancia del punto  P (3, 1, 7) al plano π: x-3y+5z-1=0  es:

7.3.4.- Distancia entre dos rectas

La distancia entre dos rectas, r y s, se puede calcular a través de la siguiente expresión:

 

(donde P y Q son puntos cualquiera de r y s respectivamente)

• Ejemplo:

Calcular la distancia entre las rectas r y s:

Obtenemos los vectores directores de ambas rectas y punto cualquiera de ambas:

Calculamos el vector PQ

Por tanto:

7.3.5.- Distancia entre una recta y un plano

• Si la recta y el plano se cortan, la distancia es cero
• Si r es paralelo a π y P es un  punto de π, dist (r, π) = dist (P, π)

7.3.6.- Distancia entre dos planos

• Si dos planos se cortan la distancia entre ellos es cero.
• Si π es paralelo a π’ y P es un  punto de π, dist (π, π’) = dist (P, π’)

Sigue estudiando!!! continúa con el apartado 7.4.- "Medidas de áreas y volúmenes"