Junio 2014: Opción A
Ejercicio 2
La función de beneficios f, en miles de euros, de una empresa depende de la cantidad invertida x, en miles de euros, en un determinado proyecto de innovación y viene dada por
a) Determine la inversión que maximiza el beneficio de la empresa y calcule dicho beneficio óptimo.
b) Calcule f'(7) e interprete el signo del resultado.
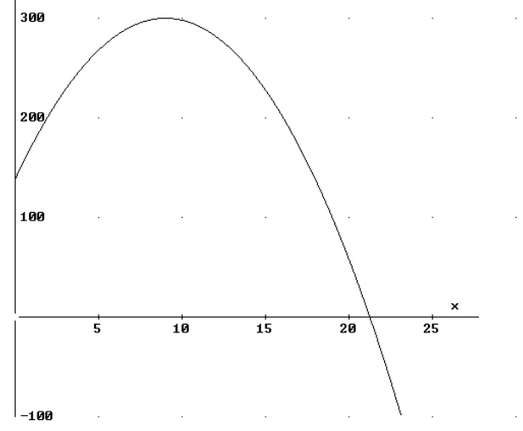
c) Dibuje la función de beneficios f(x). ¿Para qué valor o valores de la inversión, x, el beneficio es de 138 mil euros)?.
Solución
a) Se calcula la primera derivada y se iguala a cero:
f'(x)=–4x + 36 = 0 → x = 9
| (0,9) | (9, +∞) | |
| Signo f'(x) | + | – |
| Función | Creciente | Decreciente |
Como se puede observar en el cambio de signo, la función es creciente en el intervalo (0,9) y decreciente en el intervalo (9,+∞).
Además tiene un máximo relativo en el punto (9, 300).
Por lo tanto la solución es:
–. La inversión que maximiza el beneficio es x=9.000 €
–. El beneficio óptimo es f(9)=300.000 €
b) La solución es la siguiente:
f'(7)= −4 × 7 + 36 = 8 > 0
Como la solución de la derivada en ese punto es positiva, la función es creciente en dicho punto.
c) Se dibuja la función de la siguiente manera:
Después se calculan los valores de x donde el beneficio es de 138.000 €.
f(x)= −2×2 + 36x + 138 = 138
-2×2 + 36x = 0 → x=0; x=18
Por lo tanto, la solución es la siguiente:
Se obtiene un beneficio de 138.000 € con una inversión de 0 € y 18.000 €.
Recuerda la teoría:
>> Apartado 10.2 "Información extraída de la primera derivada"
Sigue jugando y ganando confianza haciendo los Ejercicios de Selectividad Matemáticas CCSS!!! "Junio 2014: Opcion B: Ejercicio 2"