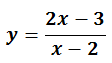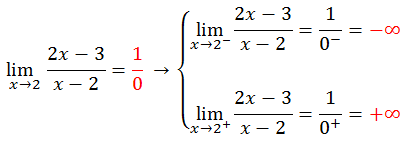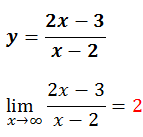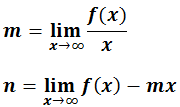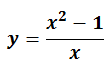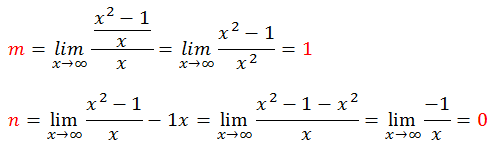Asíntota vertical
Una función tiene asíntota vertical en x=k si se cumple que:
k es el valor que anula el denominador en las funciones racionales.
Se considera que el resultado del límite es ∞ cuando el cociente resultante es un número real partido por cero.
- Ejemplo:
– En x=2 hay asíntota vertical.
Asíntota horizontal
Una función tiene asíntota vertical en y=k si se cumple que:
k es el valor que anula el denominador en las funciones racionales.
Se considera que el resultado del límite es ∞ cuando el cociente resultante es un número real partido por cero.
- Ejemplo:
– En y=2 hay asíntota horizontal.
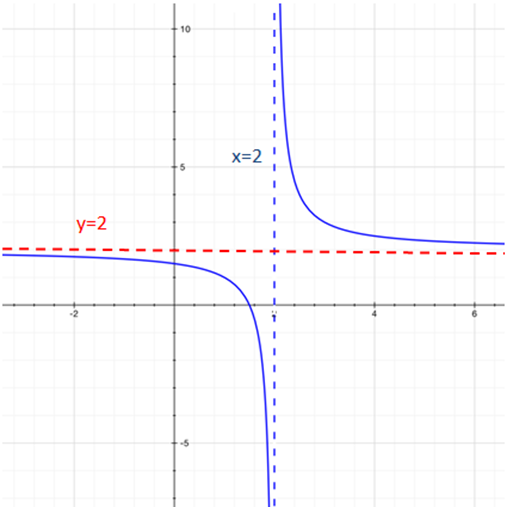
Por tanto esta función tiene una asíntota vertical en x=2 (resuelta en el punto anterior) y una asíntota horizontal en y=2 :
Asíntota oblicua
Para que una función tenga asíntota oblicua el grado del numerador debe ser exactamente un grado mayor que el del denominador.
Si una función tiene asíntota horizontal no puede tener asíntota oblicua.
Las asíntotas oblicuas son de la forma y=mx+n , donde:
- Ejemplo:
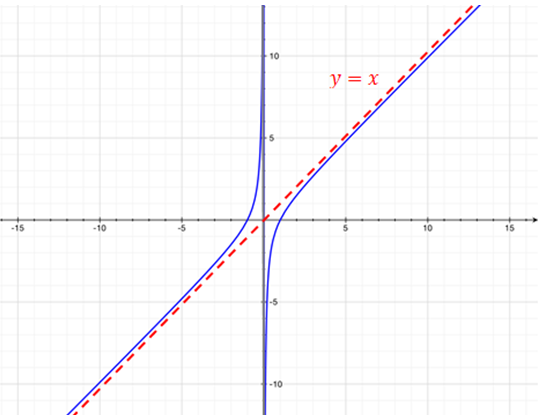
– La función tiene una asíntota oblicua en y=x :
Sigue estudiando!!! continúa con el apartado 11.5.- Crecimiento y Decrecimiento de una función