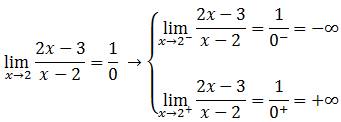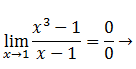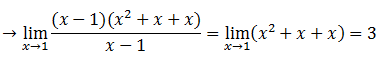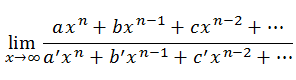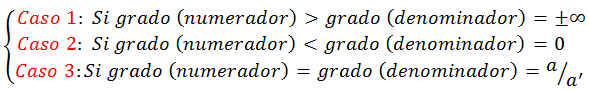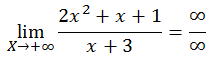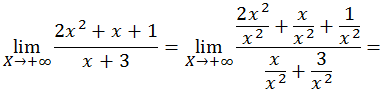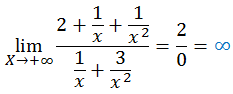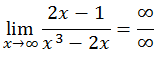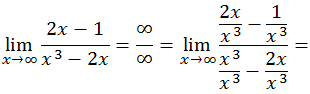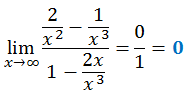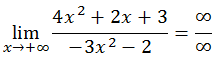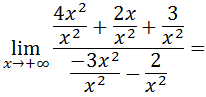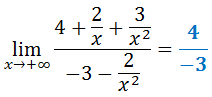2.- Límites de funciones racionales

En las funciones relacionales aparecen tres tipos de indeterminaciones.

• Indeterminación K/0 (si K≠0)

Esta indeterminación se elimina realizando los limites laterales; si son iguales la función tiene limite +∞ o –∞ ; en caso contrario no existe el límite.

• Ejemplo:

Al ser distintos los límites laterales, la función no tiene límite en ese punto.

• Indeterminación 0/0

Esta indeterminación se resuelve factorizando tanto el numerador como el denominador y posteriormente simplificando.

• Ejemplo:

• Indeterminación ∞/∞

La indeterminación ∞/∞ de funciones racionales desaparece dividiendo numerador y denominador por la máxima potencia de la función.

Para este tipo de indeterminaciones se obtendrán tres tipos de resultados en función de los grados del numerador y del denominador.  De esta forma, se podrá conocer el resultado del límite de antemano sabiendo que:

• Ejemplo:

-. Caso 1 (Si grado numerador > grado denominador) : 

Dividimos la expresión por la potencia máxima de x (en este caso x²),

-. Caso 2 (Si grado numerador < grado denominador) : 

Dividimos la expresión por la potencia máxima de x (en este caso x³),

-. Caso 3 (Si grado numerador = grado denominador) : 

Dividimos la expresión por la potencia máxima de x (en este caso x²),

Sigue estudiando!!! continúa con el apartado 3.- "Límites de funciones Irracionales"