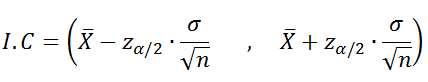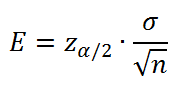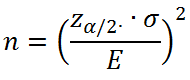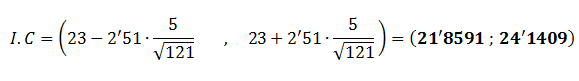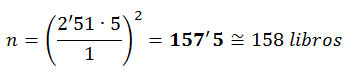12.2.1. Intervalo de Confianza
La fórmula del intervalo de confianza es:
donde,
X= media de la muestra
n= tamaño de la muestra
σ= desviación típica de la población
α= nivel de significación
12.2.2. Error de Estimación
La fórmula del error de estimación es:
12.2.3. Tamaño de la Muestra
La fórmula del tamaño de la muestra es:
- Ejemplo:
Se quiere hacer un estudio de mercado para conocer el precio medio de los libros de narrativa que se venden en la actualidad. Para ello se elige una muestra aleatoria de 121 libros, encontrando que tienen un precio medio de 23 €. Se sabe que el precio de los libros de narrativa sigue una distribución Normal con media desconocida y desviación típica 5 €.
a) Obtenga un intervalo de confianza al 98’8 %, para el precio medio de esos libros.
b) ¿Cuántos libros habría que elegir como muestra para que, con la misma confianza, el error máximo de la estimación no excediera de 1 €?
a) Del enunciado del problema se obtienen los siguientes datos:
X= media de la muestra=23
n= tamaño de la muestra=121
σ= desviación típica de la población=5
α= nivel de significación=98.8% = 1–α
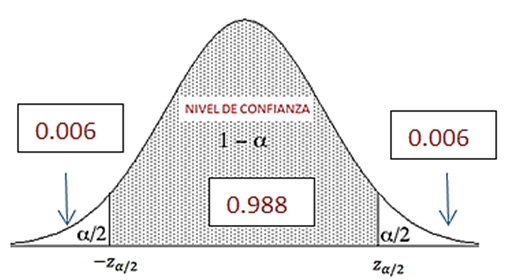
A partir del intervalo de confianza hay que obtener el valor de zα/2 . Como el nivel de confianza es 0.988, teniendo en cuenta que al área bajo la cuerva es 1, el área restante a ambos lados debe ser de valor 0.006:
Por tanto,
Aplicando la fórmula del Intervalo de Confianza (I.C) tenemos la solución:
b) Vamos a resolver la segunda cuestión,
Aplicamos la fórmula del tamaño de la muestra (n) a partir del error de la estimación es E=1 para obtener la solución:
Sigue estudiando!!! continúa con el apartado 12.3.- "Estimación de la Proporción"