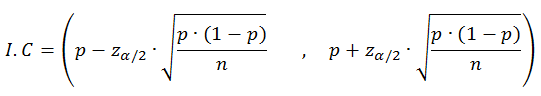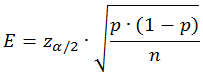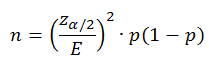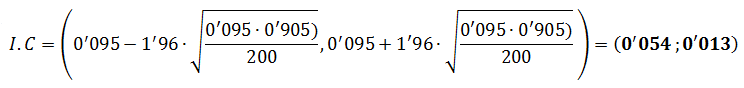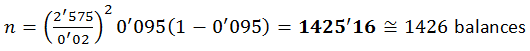12.3.1. Intervalo de Confianza
La fórmula del intervalo de confianza para la estimación de proporción es:
donde,
p= proporción de la muestra
n= tamaño de la muestra
α= nivel de significación
12.3.2. Error de Estimación
La fórmula del error de estimación para la estimación de proporción es:
12.3.3. Tamaño de la Muestra
La fórmula del tamaño de la muestra para la estimación de proporción es:
- Ejemplo:
Para estimar la proporción de balances contables incorrectos de un banco, se seleccionan aleatoriamente 200 balances, y se encuentran que 19 de ellos son incorrectos.
a) Obtenga un intervalo de confianza, al 95%, para la proporción de balances incorrectos.
b) ¿Cuántos balances se deberán seleccionar para que, con un nivel de confianza del 99%, el error de la estimación no sea superior a 0’02?
a) Del enunciado del problema obtenemos los siguientes datos:
p= proporción de la muestra= 19/200= 0.095
n= tamaño de la muestra=20
Nivel de confianza=95% = 1–α
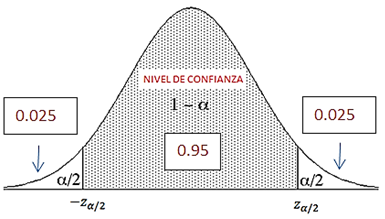
A partir del intervalo de confianza hay que obtener el valor de zα/2 . Como el nivel de confianza es 0.95, teniendo en cuenta que al área bajo la cuerva es 1, el área restante a ambos lados debe ser de valor 0.025:
Por tanto,
Aplicando la fórmula del Intervalo de Confianza (I.C) tenemos la solución:
b) Vamos a resolver la segunda cuestión, para este apartado el nivel de confianza es 0.99. Teniendo en cuenta que al área bajo la cuerva es 1, el área restante a ambos lados debe ser de valor 0.005.
Aplicamos la fórmula del tamaño de la muestra (n) para obtener la solución:
Sigue estudiando!!! continúa con el apartado 12.4.- "Contraste de Hipótesis"