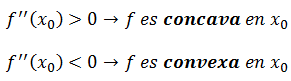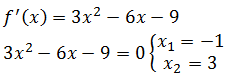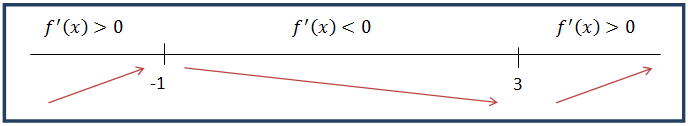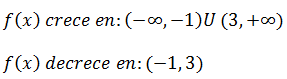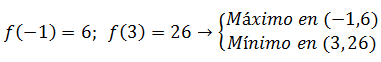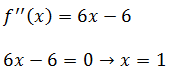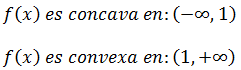(función Cóncava, Convexa)
Mediante la segunda derivada se puede determinar si una función es cóncava o convexa en un punto determinado:
Si f(x) tiene un máximo o un mínimo en x0 entonces:
- Ejemplo:
Hallar intervalos de crecimiento, máximos, mínimos, y puntos de inflexión de la siguiente función f(x),
1.- Calculamos la primera derivada y la igualamos a cero:
2.- Estudiamos el signo de la primera derivada para calcular los intervalos de crecimiento para obtener así los posibles máximos y mínimos de la función:
– Intervalos de crecimiento:
La función tiene un máximo en x = -1 y un mínimo en x = 3
Para calcular la coordenada «y»=f(x) del máximo y del mínimo, sustituimos los valores anteriores en la función:
3.- Calculamos la segunda derivada y la igualamos a cero:
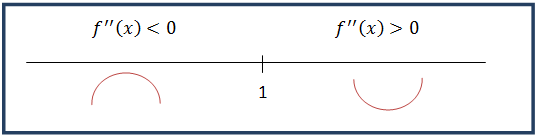
4.- Estudiamos el signo de la segunda derivada para determinar si la función es cóncava o convexa, además de obtener la coordenada del punto de inflexión:
– Intervalos de concavidad:
La función tiene un punto de inflexión en el punto x=1 . Para calcular la coordenada “y”=f(x) del punto de inflexión:
Es decir la función tiene un punto de inflexión en la coordenada (1, -10)
Sigue estudiando!!! continúa con el apartado 10.4.- "Optimización de Funciones"