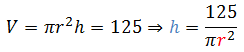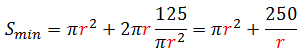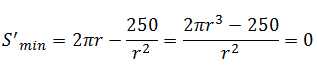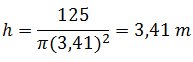Para resolver problemas de optimización de funciones hay que seguir los siguientes pasos:
- Obtener la función que se quiere maximizar o minimizar. Esta función va a depender siempre de dos incógnitas/variables.
- Utilizar los datos que proporciona el problema para que la ecuación anterior pase a depender sólo y exclusivamente de una incógnita.
- Derivar dicha función y obtener los extremos relativos. En caso de que exista un máximo y un mínimo, seleccionar el valor adecuado en función de si el enunciado del problema especifica maximizar o minimizar.
- Ejemplo:
Se desea construir un depósito en forma de cilindro recto, con base circular y sin tapadera, que tenga una capacidad de 125 m 3.
Halla el radio de la base y la altura que debe tener el depósito para que la superficie sea mínima.
1.- Obtenemos la función (depende de dos variables) que queremos que sea mínima:
2.- La función anterior depende de dos variables, “r” y “h”. Con los datos proporcionados en el enunciado del problema buscamos la relación entre las variables:
3.- Expresamos la función que queremos que sea mínima para que dependa únicamente de una sola variable:
4.- Derivamos e igualamos a cero:
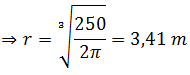
Las dimensiones mínimas del depósito son r=3,41m y h=3,41m
Sigue estudiando!!! continúa con el apartado 10.5.- "Regla de L’HÔPITAL"