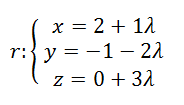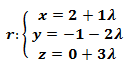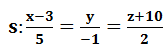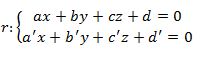Contenidos
7.1.- Direcciones de rectas y planos
7.1.1.- Dirección de una recta dada en paramétricas
La dirección de una recta viene determinada por su vector director
- Ejemplo:
Sea r la recta dada su vector director es (-2,1,0)
7.1.2.- Dirección de un plano dado en forma implícita
La dirección de un plano viene determinada por su vector normal (perpendicular) a él. Si el plano viene expresado en forma implícita:
El vector de coordenadas (a,b,c) es perpendicular al plano.
Para hallar la ecuación de un plano π, del que conocemos un punto P(Xo, Yo, Zo) y su vector normal (a,b,c) se puede proceder de la siguiente forma:
- Ejemplo:
El plano π que pasa por (5,-2,3) y es perpendicular al vector (7,1,-4) es:
7.1.3.- Plano paralelo a dos rectas
Si el plano π es paralelo a las rectas r y r’ , cuyos vectores directores son d y d’ , entonces un vector normal a π es dxd’.
- Ejemplo:
El plano π que pasa por P (3,-7,4) y es paralelo a las rectas:
Se obtiene de la siguiente forma
-. Obtenemos el vector normal del plano como:
-. Ecuación de π :
7.1.4.- Recta definida por dos planos
Cuando la recta se define en forma implícita (como intersección de dos planos):
El vector director de la recta se puede obtener como:
Sigue estudiando!!! continúa con el apartado 7.2.- "Medidas de ángulos entre rectas y planos"