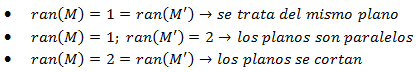6.5.- Posiciones relativas de rectas y planos
6.5.1.- Posiciones entre dos planos
Para estudiar la posición relativa de dos planos utilizaremos el rango de matrices. Para ello, dispondremos de los planos en su ecuación implícita:
Este sistema da lugar a las siguientes matrices M y M’ :
Por tanto:
6.5.1.-Posiciones entre una recta y un plano
Suponiendo que se tiene una recta r, de vector director d, y un plano π de vector normal n, pueden darse los siguientes casos:
- La recta es paralela al plano o está contenida en él.
- La recta corta al plano.
Felicidades!!! Finalizaste la Teoría de Puntos, Rectas y Planos en el Espacio!!! Ahora puedes divertirte haciendo los Ejercicios Tipo ;)