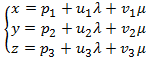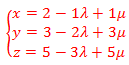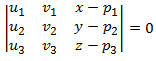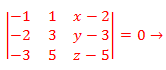Contenidos
6.4.- Ecuaciones del plano
Para expresar la ecuación de un plano se debe conocer alguna de las condiciones siguientes:
- Un punto P por el que pase el plano, y dos vectores paralelos al plano e independientes entre sí, u y v.
- Un punto P por el que pase el plano, y un vector normal (perpendicular a dicho plano) n.
Para explicar cada una de las ecuaciones de un plano, utilizaremos los siguientes datos:
- Punto por el que pasa el plano: P (2, 3, 5)
- Vectores paralelos al plano e independientes entre si:
6.4.1.- Ecuación vectorial
6.4.2.- Ecuación implícita
Donde a, b, c son las coordenadas de vector normal del plano n.
Para llegar a la ecuación implica a partir de la ecuación paramétrica es necesario resolver el siguiente determinante.
Siguiendo con el ejemplo anterior:
6.4.3.- Ecuación de un plano conocido un punto P y un vector normal n
Sean,
La ecuación resultante es:
Sigue estudiando!!! continúa con el apartado 6.5.- "Posiciones relativas de rectas y planos"