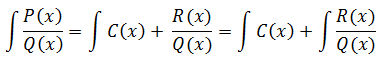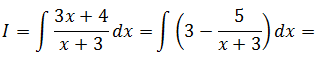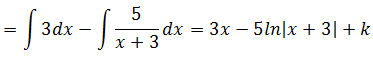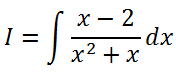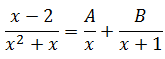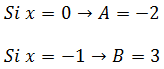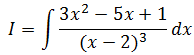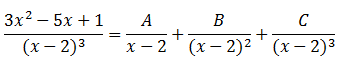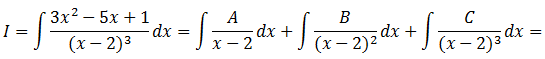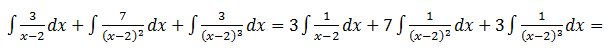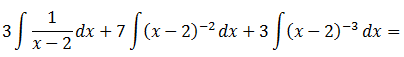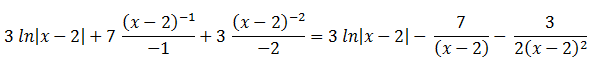Este conjunto de integrales está formado por la división de polinomios:
Se pueden dar los siguientes casos:
1. Si el numerador es de grado mayor o igual al denominador
2. Si el numerador es de grado inferior al denominador
1- Grado: Numerador >= Denominador
Si el numerador es de grado mayor o igual al denominador, se efectuará la división de polinomios correspondiente, de tal forma que la integral quedará trasformada en otras dos más sencillas:
donde R(x) es el resto de la división y C(x) el cociente
- Ejemplo:
2- Grado: Numerador < Denominador
Si el numerador es de grado inferior al denominador, hay que descomponer en fracciones el cociente.
En este caso se puede suceder lo siguiente:
a) El denominador solo tiene raíces reales sencillas
b) El denominador tiene raíces reales múltiples
- Ejemplo 2.a): «El denominador solo tiene raíces reales sencillas»
El denominador solo tiene raíces sencillas (x=0 y x=-1).
Descomponemos el denominador en factores (sacamos factor común),
A cada factor le asignamos una variable en el numerador (A y B en el ejemplo),
Resolvemos la ecuación aplicando mínimo común múltiplo,
Calculamos A y B asignándole valores a la x (por facilidad de cálculo siempre le daremos los valores de las raíces del denominador),
Por tanto,
- Ejemplo 2.b): «El denominador tiene raíces reales múltiples»
En este caso, el denominador tiene tres raíces iguales (x=2). El proceso de resolución es igual que en el caso anterior, solo que al descomponer la fracción algebraica se obtienen tantas fracciones como el orden de multiplicidad de la raíz (tres en este caso):
Resolvemos la ecuación:
Calculamos las variables A, B y C asignándole valores a x :
Por tanto:
Felicidades!!! Finalizaste la Teoría de Cálculo de Primitivas Integrales!!! Ahora puedes divertirte haciendo los Ejercicios Tipo ;)