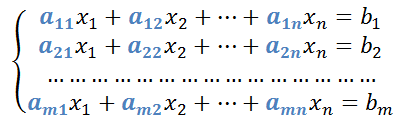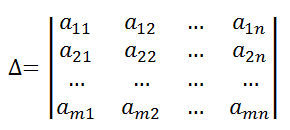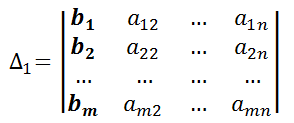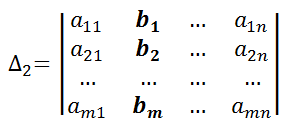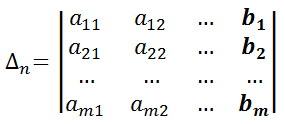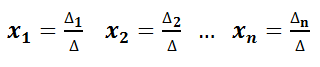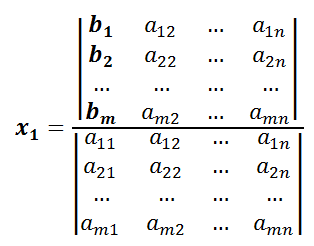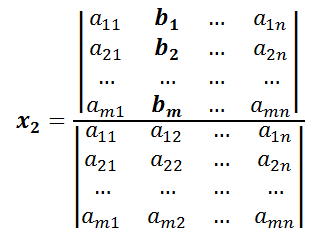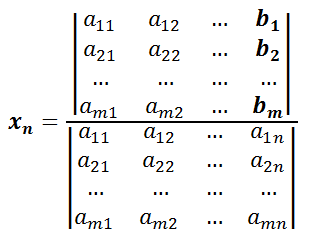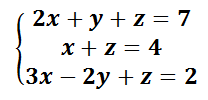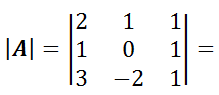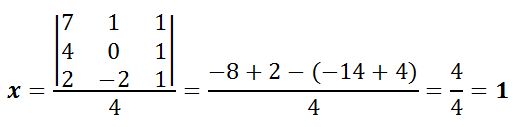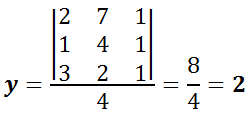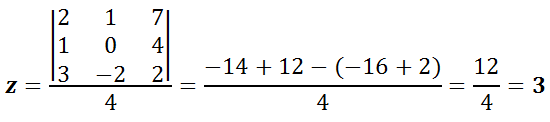4.1.- Método de Cramer
La regla de Cramer se aplica para resolver sistemas de ecuaciones lineales que cumplan las siguientes condiciones:
– El número de ecuaciones es igual al número de incógnitas.
– El determinante de la matriz de los coeficientes debe ser distinto de cero.
Los que cumplan ambas condiciones son sistemas compatibles determinados denominados como sistemas de Cramer.
Los que cumplan ambas condiciones son sistemas compatibles determinados denominados como sistemas de Cramer.
Sea Δ el determinante de la matriz de coeficientes del sistema:
Sea Δ1, Δ2, … Δn son los determinantes de la matriz formada por la matriz de coeficientes y la columna con los resultados ( b1, b2 … bn ) del sistema.
…
Un sistema de Cramer puede tener sólo y exclusivamente una única solución (ya que es un sistema compatible determinado).
Para obtener las soluciones x1, x2, … xn hay que resolver la siguiente fórmula:
…
- Ejemplo:
– Solución –> (x, y, z) = (1, 2, 3)
Felicidades!!! Finalizaste la Teoría de Resolución de Sistemas de Ecuaciones Lineales por el Método de Cramer!!! Si quieres seguir practicando y divirtiéndote con las Mates, te recomendamos que te pases por la sección de Ejercicios Tipo ;)