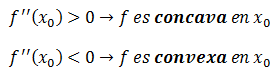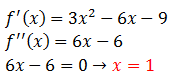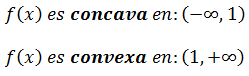Mediante la segunda derivada se puede determinar si una función es cóncava o convexa en un punto determinado:
Para calcular los intervalos de concavidad y convexidad de una función hay que seguir los siguientes pasos:
- Hallar el dominio de la función.
- Calcular la segunda derivada e igualarla a cero.
- Dibujar en una tabla los valores que hayamos obtenido de igualar la segunda derivada a cero y aquellos valores que no pertenezcan al dominio de la función.
- Estudiar el signo de la segunda derivada en los intervalos que hayamos obtenido al colocar de forma ordenada los valores del apartado 3.
- Ejemplo:
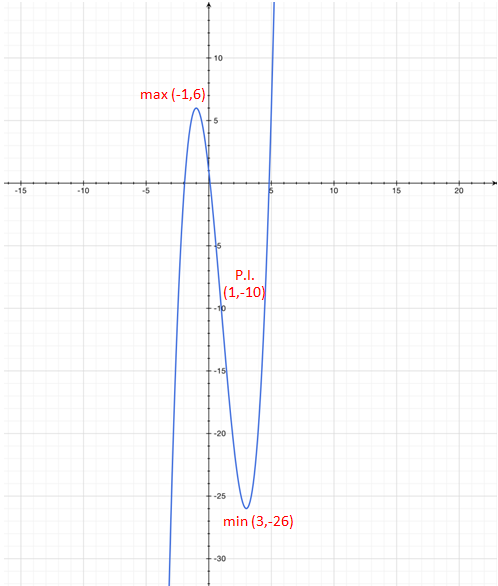
Hallar intervalos de crecimiento de la siguiente función,
1.- Dominio
2.- Se calcula la segunda derivada e igualar a cero
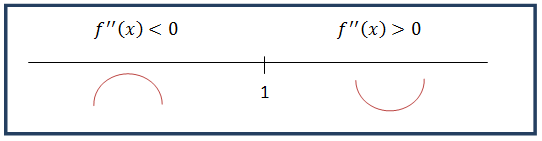
3.- Como el dominio es ℝ, se dibujan en la tabla únicamente los valores que se han obtenido al igualar la segunda derivada a cero ( x =1 ).
4.- Estudiamos el signo de la segunda derivada en los intervalos resultantes:
5.- La solución es:
Punto de inflexión
Si una función pasa de cóncava a convexa en un punto o viceversa y ese punto pertenece al dominio, entonces a dicho punto se le denomina punto de inflexión.
- Ejemplo:
Siguiendo con la función del ejemplo anterior, en este caso la función tiene un punto de inflexión en x=1 . Para calcular la coordenada y del punto:
Es decir la función tiene un punto de inflexión en la coordenada (1, -10)
Felicidades!!! Finalizaste la Teoría de Derivadas!!! Ahora puedes divertirte jugando con los Ejercicios Tipo ;)