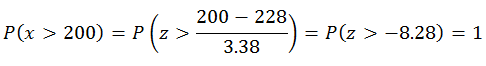Para que puedas aproximar una distribución binomial a una distribución normal, deben cumplirse dos condiciones:
- n • p ≥ 5
- n • q ≥ 5
Si se cumplen estas dos condiciones entonces la distribución binominal se puede aproximar a la siguiente distribución normal:
- Ejemplo:
En el instituto Santa Rosa de Lima en Málaga se presentan a Selectividad 240 alumnos este año. Se sabe que en este centro el porcentaje de alumnos que suelen aprobar es del 95%. Calcular la probabilidad para que aprueben más de 200 alumnos.
Obtenemos los datos a través del enunciado,
n=240;
p=0.95;
q=1-p=0.05
Se trata de una distribución binomial B(240, 0.95)
Veamos si se cumplen las dos condiciones para aproximar la distribución binomial a la normal:
1. n • p≥5 ⇒ 240 • 0.95≥5 OK (se cumple)
2. n • q≥5 ⇒ 240 • 0.95≥5 OK (se cumple)
Por tanto sí se puede aproximar a la siguiente distribución normal :
Solución:
Con esta distribución calculamos la probabilidad para que aprueben más de 200 alumnos
Felicidades!!! Finalizaste el tema de Distribuciones!!! Ahora puedes divertirte jugando con los Ejercicios Tipo ;)