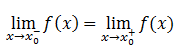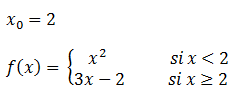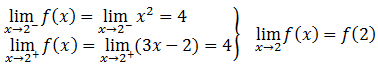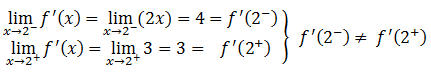Tema 9: Derivadas y Técnicas de Derivadas

9.3.- Derivabilidad de una función definida a trozos

Para que una función f sea derivable en un punto x₀ , primero ha de ser continua en dicho punto. Si es continua, es posible que la función sea derivable o no. Para que sea derivable sus límites laterales deben coincidir, es decir:

• Ejemplo:

Estudiar la derivabilidad en x₀ = 2 de la siguiente función f(x),

Para que f(x) sea derivable en x = 2 , primero tiene que ser continua en ese punto, por tanto vamos a comprobar su continuidad,

-. Continuidad en x₀ = 2

Por tanto f(x) es continua en x₀ = 2

-. Derivabilidad en x₀ = 2

Las derivadas laterales existen pero no coinciden. Por tanto, la función no es derivable en x₀ = 2

Felicidades!!! Finalizaste la Teoría de Derivadas!!!
Ahora puedes divertirte jugando con los Ejercicios Tipo ;)