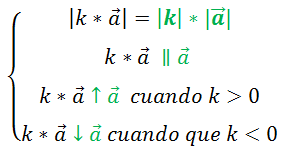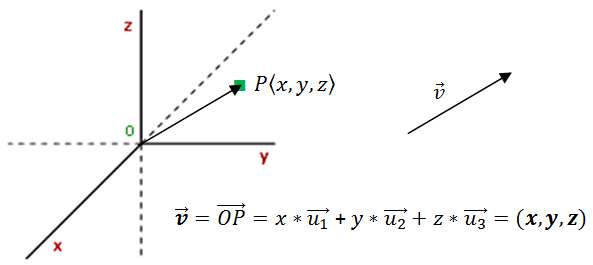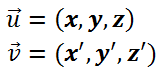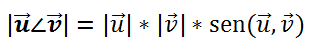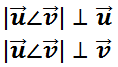Contenidos
5.4- Operaciones de un Vector en el Espacio
Las operaciones de un vector en el espacio son:
- Suma
- Producto de un número por un vector
- Producto escalar
- Producto vectorial
- Producto mixto
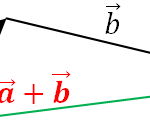
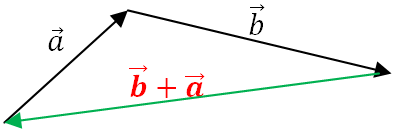
5.4.1- Suma
5.4.2- Producto de un número por un vector
- Nota :
Las operaciones Suma y Producto de un número por un vector, sirven para pasar los vectores del “dibujo” a números.
Con estas dos operaciones y con el concepto “Sistema de Referencia” o (s.d.r) es posible convertir los problemas vectoriales en problemas numéricos. De esta forma se transforma el problema vectorial desde un sistema descriptivo (dibujo) a un sistema analítico, gracias a las coordenadas cartesianas.
Además con los s.d.r es posible dotar de coordenadas a los puntos del espacio. Cada punto P del espacio se puede considerar el extremo de un vector que tiene como origen O, llamado vector posición.
5.4.3- Producto escalar
El resultado de un producto escalar es un número, se calcula a partir del producto del módulo de ambos vectores por el coseno del ángulo que forman ambos vectores.
La fórmula es:
- Nota :
La expresión del cálculo analítico del producto escalar es bastante laborioso. Con el fin de simplificarlo, para calcular el producto escalar se utilizan unas bases que simplifican el cálculo de los productos escalares. Estas bases son las llamadas bases “orto-normales”, dos vectores son orto-normales si:
-. Ambos vectores son perpendiculares (ortogonales)
-. Módulo de ambos vale la unidad
- Ejemplo:
Teniendo en cuenta la Nota anterior, si disponemos de 2 vectores orto-normales
5.4.4- Producto vectorial
La fórmula del producto vectorial es la siguiente:
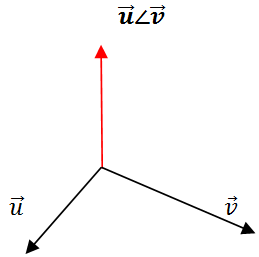
Siendo el resultado,
- Nota :
Utiliza la regla del “tornillo” o del “sacacorchos” para dibujar el resultado del producto vectorial.
5.4.5- Producto mixto
La fórmula del producto mixto es la siguiente:
Felicidades!!! Finalizaste la Teoría de Vectores en el Espacio!!! Ahora puedes divertirte haciendo los Ejercicios Tipo ;)