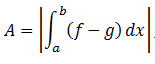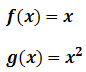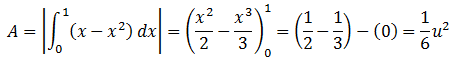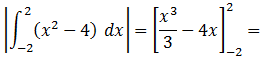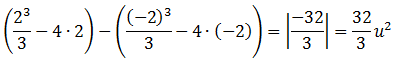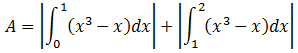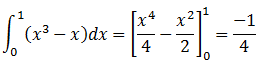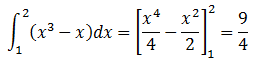Cálculo de área: 2 funciones
El área comprendida entre dos funciones se puede calcular mediante la siguiente expresión:
(siendo a y b los puntos de corte de ambas funciones)
- Ejemplo: «Hallar el área comprendida entre las curvas»
Se calculan los puntos de corte de ambas funciones. Para ello se igualan entre sí y se resuelve la ecuación resultante:
Por tanto, el área encerrada por las dos funciones es:
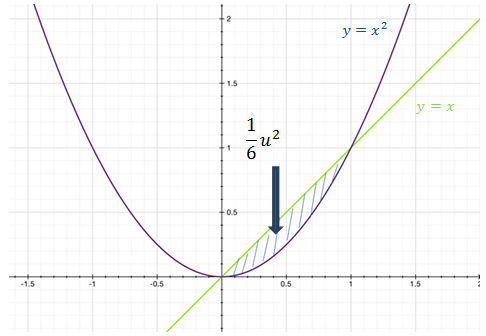
Gráficamente el área calculada se muestra a continuación:
Cálculo de área: una función y el eje
- Ejemplos: «Calcular el área comprendida entre la función y=x2–4 y el eje OX«
Este es un caso particular del área comprendida entre dos funciones, donde una de las dos funciones es el eje x, es decir la función y=0 .
Para calcular el área comprendida entre una función cualquiera y el eje x, lo primero que hay que hacer es calcular los puntos de corte de dicha función con el eje x. Para ello igualamos la función a cero y resolvemos:
El siguiente paso es calcular la integral en valor absoluto de la función entre los puntos obtenidos, ya que el área nunca puede dar como resultado un valor negativo:
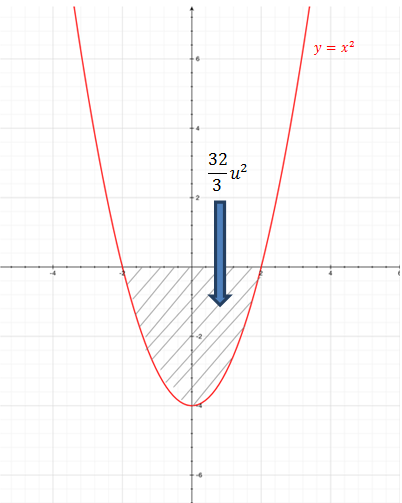
Gráficamente el área calculada se muestra en la siguiente imagen:
Cálculo de área: una función, eje X, 2 rectas
- Ejemplos: «Calcular el área comprendida entre la curva y=x3–x, el eje X y las rectas x=0 y x=2.
Las rectas dadas (x=0 y x=2) van a delimitar el intervalo de integración. Sin embargo, se deben calcular los puntos de corte entre la función dada y el eje OX para saber si en ese intervalo, existe algún punto de corte intermedio que debe tenerse en cuenta al integrar.
Para calcular los puntos de corte se iguala la función a cero y se resuelve la ecuación,
Se observa que uno de los puntos de corte está dentro del intervalo de integración, concretamente el punto x=1. Por tanto para obtener el área requerida habrá que calcular:
Calculamos cada una de ellas por separado:
Por tanto la solución es:
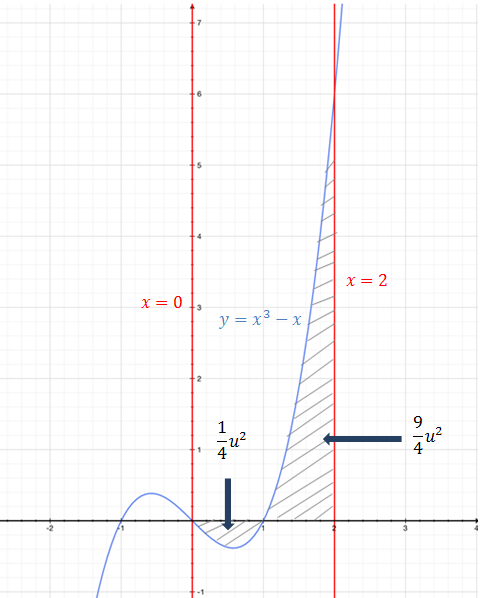
Gráficamente el área obtenida se muestra en la siguiente imagen:
Sigue estudiando!!! continúa con el apartado 13.3.- Volumen de un cuerpo de revolución