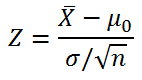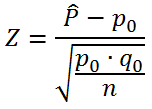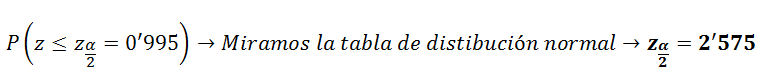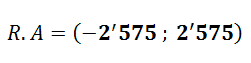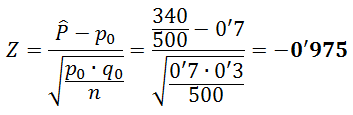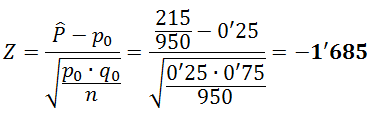Un contraste de hipótesis es un procedimiento para determinar si una afirmación o característica de una población puede ser admitida o rechazada y con qué error (nivel de significación) se puede aceptar o rechazar.
La hipótesis emitida recibe el nombre de hipótesis nula, H0.
La hipótesis contraria se designa por H1 y se denomina hipótesis alternativa.
Para realizar un contraste de hipótesis se seguirán los siguientes pasos:
Contenidos
1. Enunciar las hipótesis
- Hipótesis Unilateral
Por la izquierda: H0 ≥ K ; H1 < K
Por la derecha: H0 ≤ K ; H1 > K
- Hipótesis Bilateral
H0 = K ; H1 ≠ K
2. Construir la zona de aceptación y rechazo
A partir de un nivel de significación dado, construir la zona de aceptación y la zona de rechazo
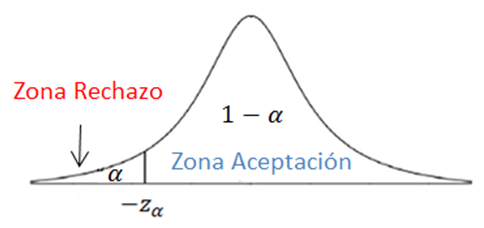
- Hipótesis Unilateral
Por la izquierda:
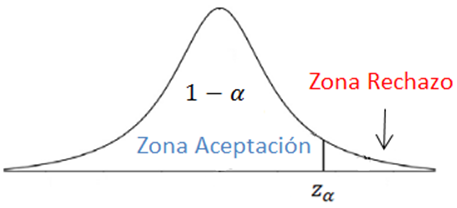
Por la derecha:
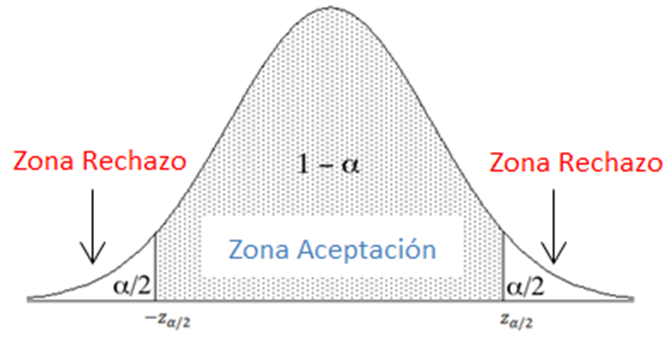
- Hipótesis Bilateral
3. Calcular el estadístico de prueba
Calculamos el estadístico de prueba, según se esté calculando medias o proporciones.
- Media
- Proporción
4. Decidir si el valor calculado está en la zona de aceptación
Decidir si el valor calculado se encuentra dentro o fuera de la zona de aceptación.
- Ejemplo A:
A) Contraste Hipótesis BILATERAL
Un titular de prensa afirma que el 70% de los jóvenes de una ciudad utilizan las redes sociales para comunicarse. Para contrastar la veracidad de tal afirmación se toma una muestra aleatoria de 500 jóvenes de esa ciudad, y se obtiene que 340 de ellos utilizan la red para comunicarse.
Analice mediante un contraste de hipótesis bilateral, si se puede aceptar, con un nivel de significación del 1%, que dicha afirmación es cierta.
1. Enunciamos la hipótesis
H0 : p = 0.7
H1 : p ≠ 0.7
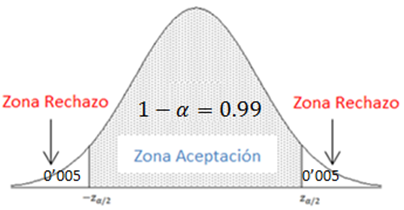
2. El contraste es bilateral.
A partir del nivel de significación (α=0.01), construimos la zona de aceptación y la zona de rechazo
Calculamos Zα/2
Por tanto la Región de Aceptación (R.A) es,
3. Calculamos el estadístico de prueba, en este caso la Proporción:
4. Como el estadístico de prueba está dentro de la región de Aceptación, Aceptamos .
La solución es: con un nivel de significación del 1%, se acepta que el 70% de los jóvenes de esa ciudad utilizan las redes sociales
- Ejemplo B:
B) Contraste Hipótesis UNILATERAL
Queremos estudiar la proporción de personas de una población que usan una determinada marca de ropa. Para ello se hace una encuesta a 950 personas y se obtiene que 215 de ellas usan esa marca. Utilizando un contraste de hipótesis (H0 : p ≥ 0.25)
¿Podemos afirmar con estos datos y con un nivel de significación del 5% que al menos el 25% de toda la población usa esa marca de ropa?
1. Enunciamos la hipótesis
H0 : p ≥ 0.25
H1 : p < 0.25
2. El contraste es unilateral.
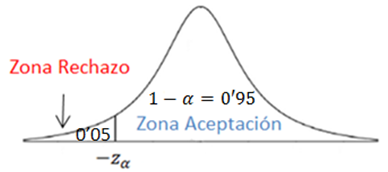
A partir del nivel de significación (α=0.05), construimos la zona de aceptación y la zona de rechazo
Calculamos Zα
Por tanto
Además, la Región de Aceptación (R.A) es
3. Calculamos el estadístico de prueba, en este caso la Proporción:
4. Como el estadístico de prueba NO está dentro de la región de Aceptación, rechazamos H0 y aceptamos H1 .
La solución es: con un nivel de significación del 5%, se puede afirmar que menos del 25% de esa población usa esa marca de ropa
Felicidades!!! Finalizaste el tema de Distribuciones!!! Ahora puedes divertirte jugando con los Ejercicios Tipo ;)